Generalized Chord-Member Intervals and Transformations

Alexander Shannon

Abstract

This article develops a theory of chord-member space, incorporating an apparatus of vertical positions into an established linearization of voice-leading principles. I propose a new methodology to describe motion that occurs when the voices of one chord reposition themselves into different positions of another chord (e.g., the root of one chord becomes the third of the next). In so doing, I generalize a chord-member space with accompanying intervals that form a discrete mod-7 group structure. I introduce the concept of heard chord members that exist within their own space and argue that this system illustrates characteristics of diatonic and chromatic progressions that are not easily detectable by previously established transformational approaches. By analyzing a sample of diatonic and chromatic musical passages from the eighteenth and nineteenth centuries, I show that one can hear changes in vertical placement as distinctive linear gestures. This system offers a novel perspective on chord progressions and voice leading, revealing subtle nuances in tertian harmony.
View PDF
Return to Volume 38

Keywords and Phrases: chord, mod-7, intervals, transformations, qualia

Introduction

Theories of transformational voice leading study relationships between musical objects, and there are multiple ways to view these relationships. Steven Rings (2011, 38) discusses a prismatic analytical approach, whereby “phenomenologically rich local passages are refracted and explored from multiple perspectives.” This is a warranted idea because musical environments often feature multiple dimensions of detail and thus multiple avenues of interpretation. Consider Example 1, showing the end of the Minuet to W. A. Mozart’s String Quartet No. 19 in C Major, K. 465 (1785): a deceptive resolution occurs in mm. 60–61 and is then followed by a perfect authentic cadence in the home key in mm. 62–63. The two instances have almost the same voiced resolutions: $$\hat{7}$$ in the first violin resolves up by half step to $$\hat{1}$$, $$\hat{2}$$ in the second violin resolves down by whole step to $$\hat{1}$$, and $$\hat{4}$$ in the viola resolves down by half step to $$\hat{3}$$. The difference, as one might expect, is found in the bass’s resolution: while it moves up by whole step to $$\hat{6}$$ in the former instance, it descends by perfect fifth to $$\hat{1}$$ in the latter. A traditional contrapuntal analysis would highlight the similarities between the two instances and would explain why the former is considered a “deceptive” resolution: it has most of the same syntax as a perfect authentic cadence, but the bass’s movement disrupts the impending sense of closure and merely prolongs the inevitable, or what we expect to be inevitable.

This analysis, however, misses how the voices achieve a sense of balance within the dominant chord and in their resolution to the tonic-functioning chord. It does not account for the voices’ sense of third-based relationships, where there is a clear designation of the “root,” and the root dictates every other voice’s chord-member location. The progression involves tertian structures exclusively, and as the chords progress, each voice transforms from one chordal position to another (e.g., from the third of one chord to the root of another). Despite the upper three voices having the same pitch-class and scale-degree resolutions between the two cadences, their changes in vertical location are not the same. The chord-member assignments for each V⁷ stay the same, but the chord-member assignments for the upper voices in the resolving chords are different because they are given different harmonic support. The two violins may be resolving to the tonic pitch each time, but only the second time do they fully resolve as the root of the tonic harmony, suggesting that there is a contrast in their closure. This chord-member reading also shows that the cello maintains its role as the harmonic root despite being the only voice that changes pitch classes and scale degrees between the two resolutions; this is in stark contrast to the upper voices, which do not change pitch classes or scale degrees but find new tertian roles. Can such a theoretical apparatus that captures this kind of chord-member information be developed and successfully replicated, and what would this kind of mechanism ultimately demonstrate about music?

In this article, I propose such a methodology for describing the chord-member voice leading of diatonic and chromatic chord progressions. Through this chord-member system, I offer a new analytical approach that allows one to hear changes in vertical placement as characteristic linear gestures, even in progressions that do not convey a clear tonal center. First, I will introduce my organizing system and its utility through several familiar short eighteenth- and nineteenth-century musical excerpts. Then, I will demonstrate its utility through extended analyses of longer passages and apply the system to the more familiar neo-Riemannian theory. Finally, I will synthesize my findings and advocate for this contribution’s salience in the field of music theory.

1. Chord Members and Chord-Member Space

I devise a system that provides an illustrative reading of transformational voice leading when voices undergo chordal repositioning. To begin, I introduce a new conceptual framework: the notion of a Generalized Interval System (GIS) called chord-member space, denoted by cm.¹ cm should not be confused with chord space, as described by Dmitri Tymoczko (2011, 65), or chordal space, as described by Fred Lerdahl (2001, 53–59). cm is a generic (mod-7), discrete apparatus of tertian chord positions in which the tertian structure is clearly defined.² For reference, cm is a generic (mod-7), discrete space, just like generic pitch-class space (gpc). As Leah Frederick (2019, 171) and Julian Hook (2023, 15–16) discuss, every element of gpc is an equivalence class of note names that share the same letter (e.g., C𝄫, C$$\natural$$, and C$$\sharp$$ all fall under the equivalence class “C” in gpc). As I will demonstrate in this article, cm has many of the same properties but some nuanced differences.

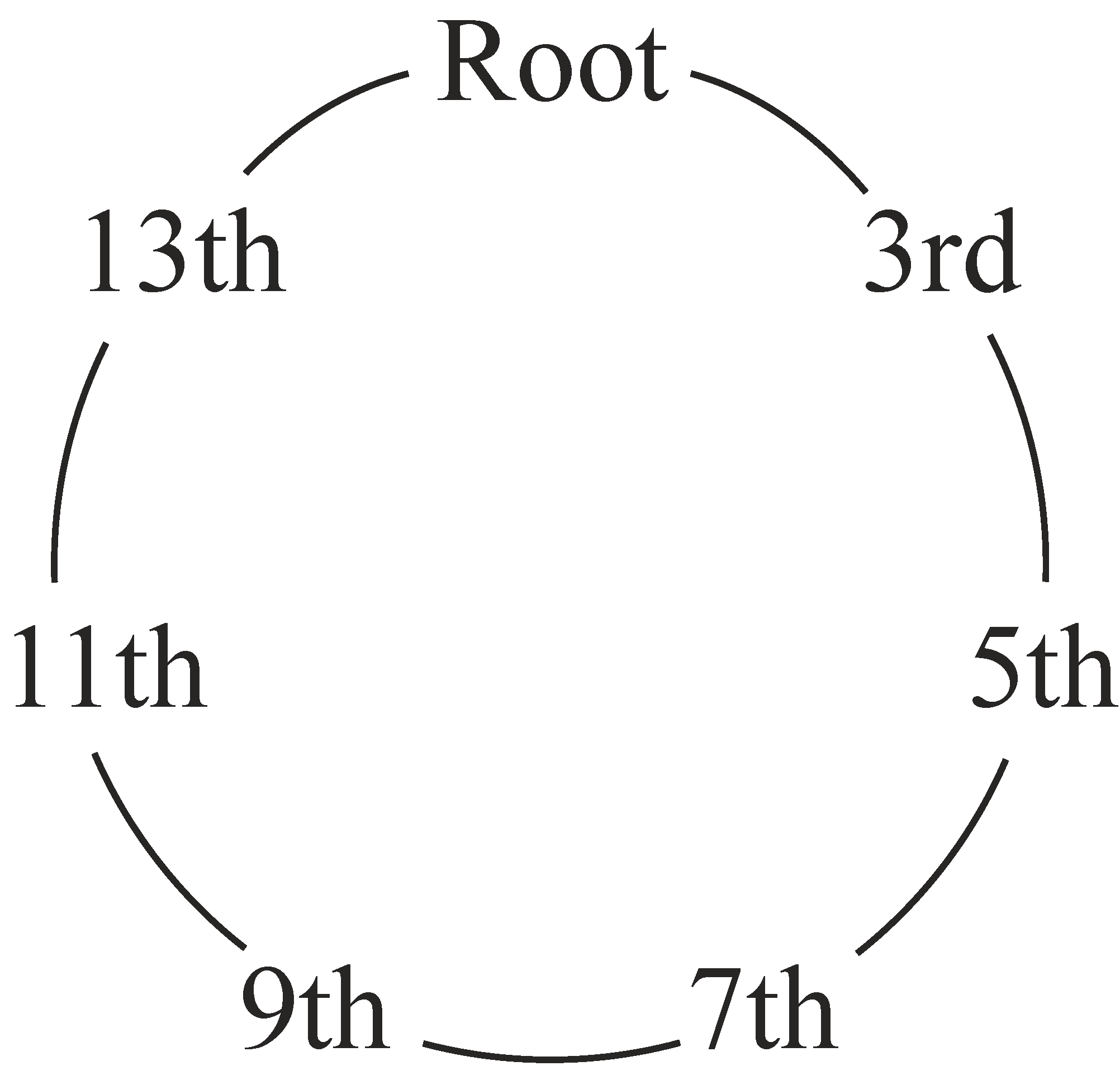
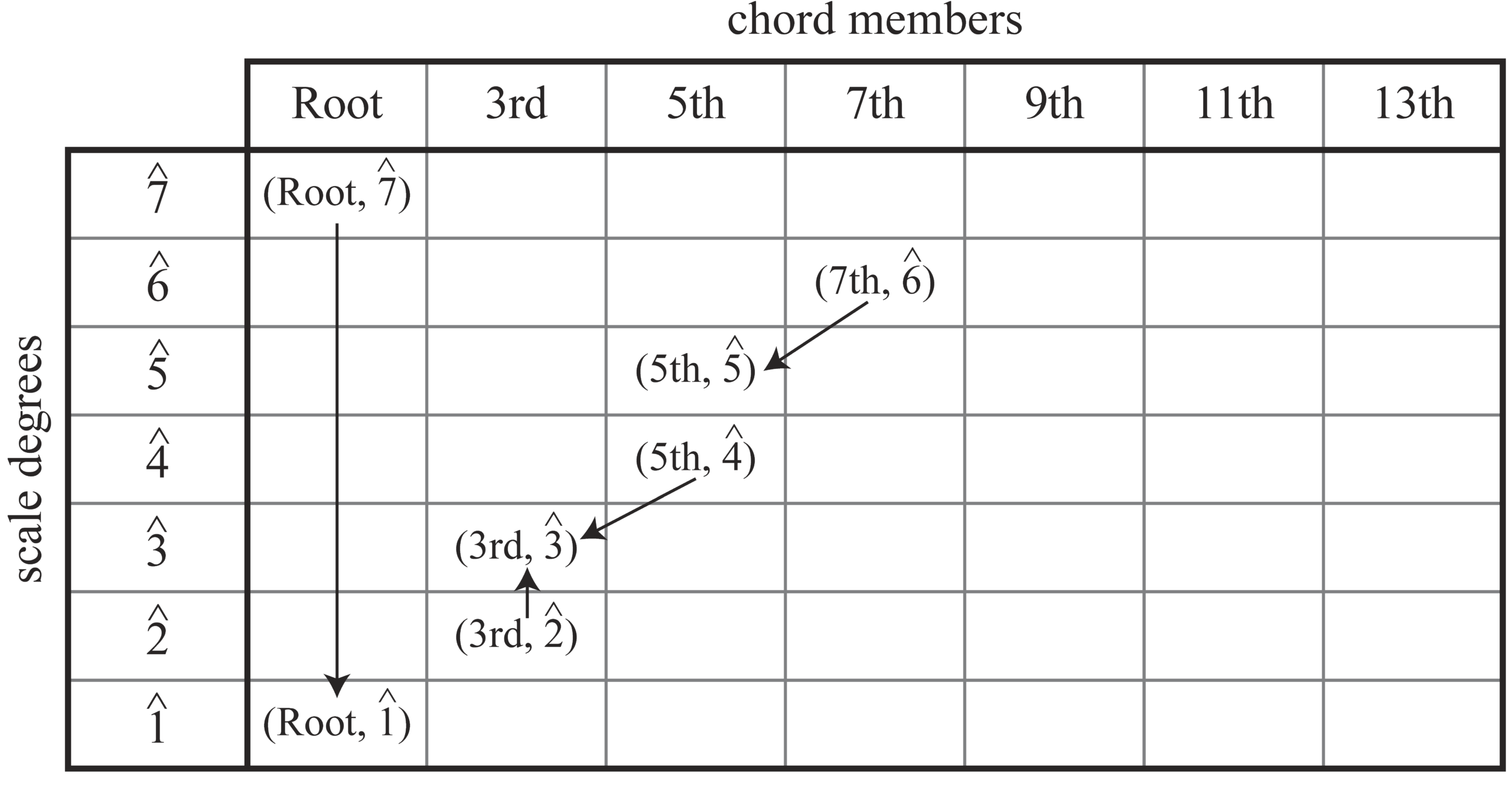
Example 2 provides a realization of the space I propose: the members of the space are the abstract elements called Root, 3rd, 5th, 7th, 9th, 11th, and 13th, which are used as labels associated with various pitches in a chord.³ Looking back at Example 1, the excerpt showed the members of the V⁷, vi, and I chords in the C-major minuet given some of these names. Any number of pitches or pitch classes can be given the same chord-member label. For example, the tonic chord’s C₂, C₄, and C₆ in Example 1 are all assigned the “Root” label. Meanwhile, a mixed-third chord (i.e., a triad with a major third and a minor third) would have two pitch classes belonging to the same chordal position, “3rd.” Each element in the space is arranged in stacked-third order, similarly to how one would sing an arpeggiation of a tertian harmony. I will discuss the interval group governing this space in more detail in the next section, but for now, the basic interval between any two consecutive chord members is denoted by a general label “3rd” (not to be confused with the chordal position “3rd”).

Related to this space is the idea of chord-member quale (or the plural form qualia), which is the perception of a chord member influenced by experience and requiring present reflection, particularly in triadic tonality and post-tonality.⁴ In many musical settings and collaborations, whether a chorus, chamber ensemble, or a standard soloist/piano accompaniment duo, the performers are often tasked with understanding how their part fits with the rest of the ensemble. The bass voice of a multi-part texture usually provides the harmonic foundation; when the bass provides the root of a triad, that sonority is likely to be perceived as resolute. If it provides the third, the sonority is less resolute, and if it provides the fifth, the sonority is often considered dissonant. Furthermore, the upper voices are tasked with tuning to the bass. It makes a world of difference if one of the said voices doubles the bass or realizes a note different from the bass. It is incumbent upon that ensemble member to understand, for example, that tuning the harmonic third is more flexible (and, in some ways, more difficult) than tuning the harmonic fifth. Therefore, our perception of a chord member is influenced by our experience and requires reflection, so this article will often discuss the quale associated with a given chord member. The idea of chord-member qualia implies that it is possible for the notes of an open-fifth chord, for example, to have the qualia of either the chordal root or fifth, even without a chordal third present.

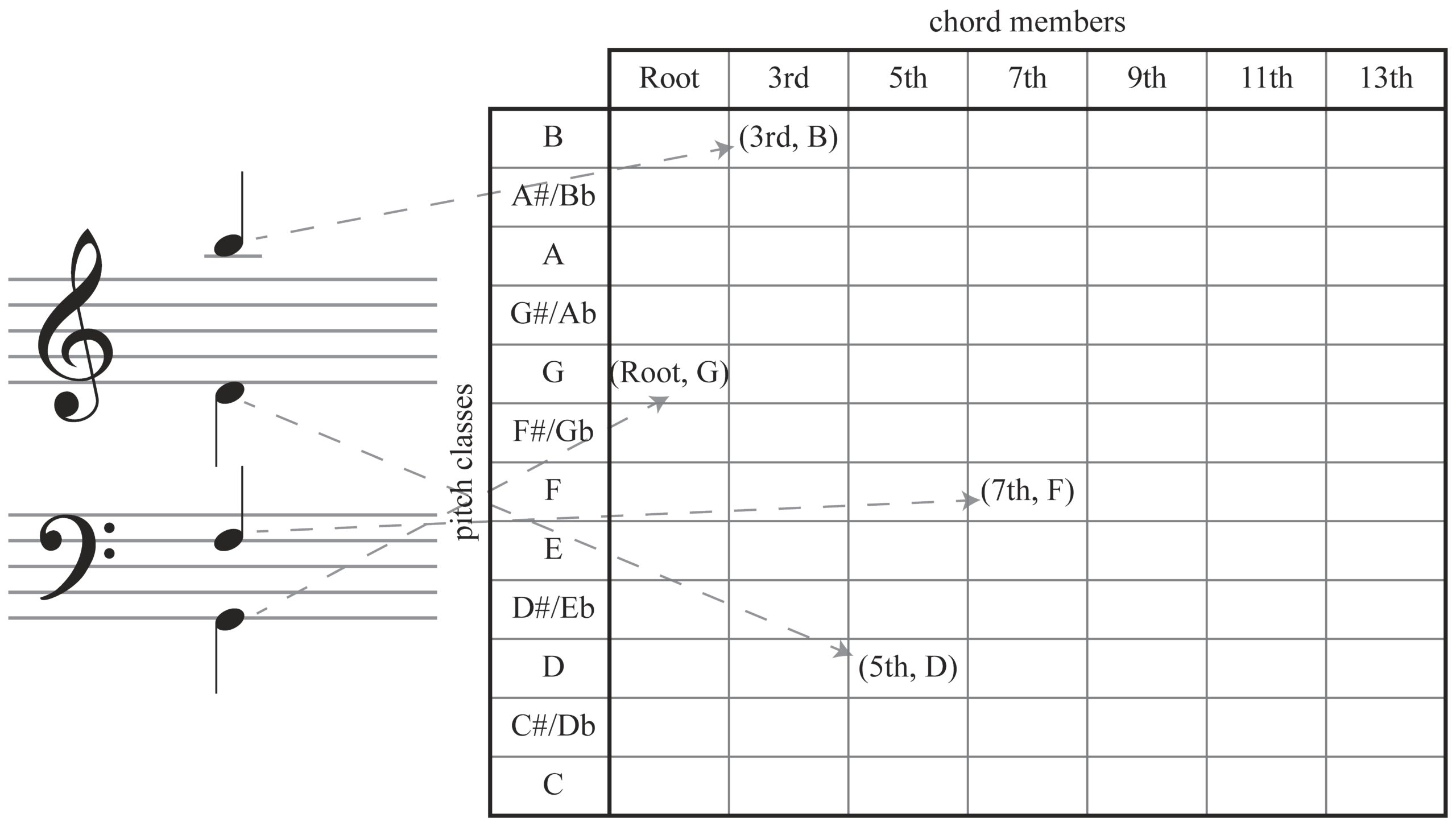
In my proposed system, one can describe any given note as an ordered pair derived from the direct product cm × pc, where cm is the newly introduced chord-member space, and pc is the usual pitch-class space. The ordered pair is of the form (cm, pc), where cm represents the heard chord member, and pc represents its regularly assigned pitch-class integer. In this GIS, cm is the space of all heard chord members, making cm × pc the space s of all 84 ordered pairs of chord members and pitch classes. Example 3 shows the V⁷ chord from Example 1 mapped onto a Rings-inspired table (2011, 45) presenting an interpretation of this space. The table’s horizontal and vertical dimensions wrap around to form a torus.

2. Chord-Member Interval Group and Interval Function

To describe the interval between two notes, I use a different ordered pair of the form (cmint, pcint), where cmint represents the ascending chordal interval by a harmonic third (the designation “3rd” represents an ascending chordal third, “3rd²” represents two ascending chordal thirds, and so on), and pcint represents the ascending chromatic interval by semitone. Chordal intervals are described from the bottom up: Root to 3rd, 3rd to 5th, and so on. One could choose to describe an interval as ascending with a positive superscript (e.g., “3rd²”) or as descending with a negative superscript (e.g., “3rd⁻²”). It is possible to simplify the notation for clarity; for example, the interval “3rd²” can be rewritten as “5th,” and the interval “3rd⁻²” can be rewritten as “5th⁻¹.” However, there are advantages to notating intervals as “3rdⁿ,” where n represents the number of chordal steps taken.

It is important to note that “3rd” denotes a generic third and does not distinguish quality (e.g., major, minor, diminished). This lack of quality distinction is where the conjoining of chord-member intervals with pitch-class intervals comes in handy: the interval (3rd, 4), for example, represents a single ascending chordal movement (i.e., “step”) by major third, whereas the interval (3rd, 3) represents an ascending chordal step by minor third. This idea of a generic chordal step seems identical to a generic melodic third, but its implications differ. The apparatuses by which these gestures are defined are different; a generic chordal step is defined by an array of positions based on a generalized tertian chord, whereas a generic melodic third is defined by an array of positions based on a generalized scale.

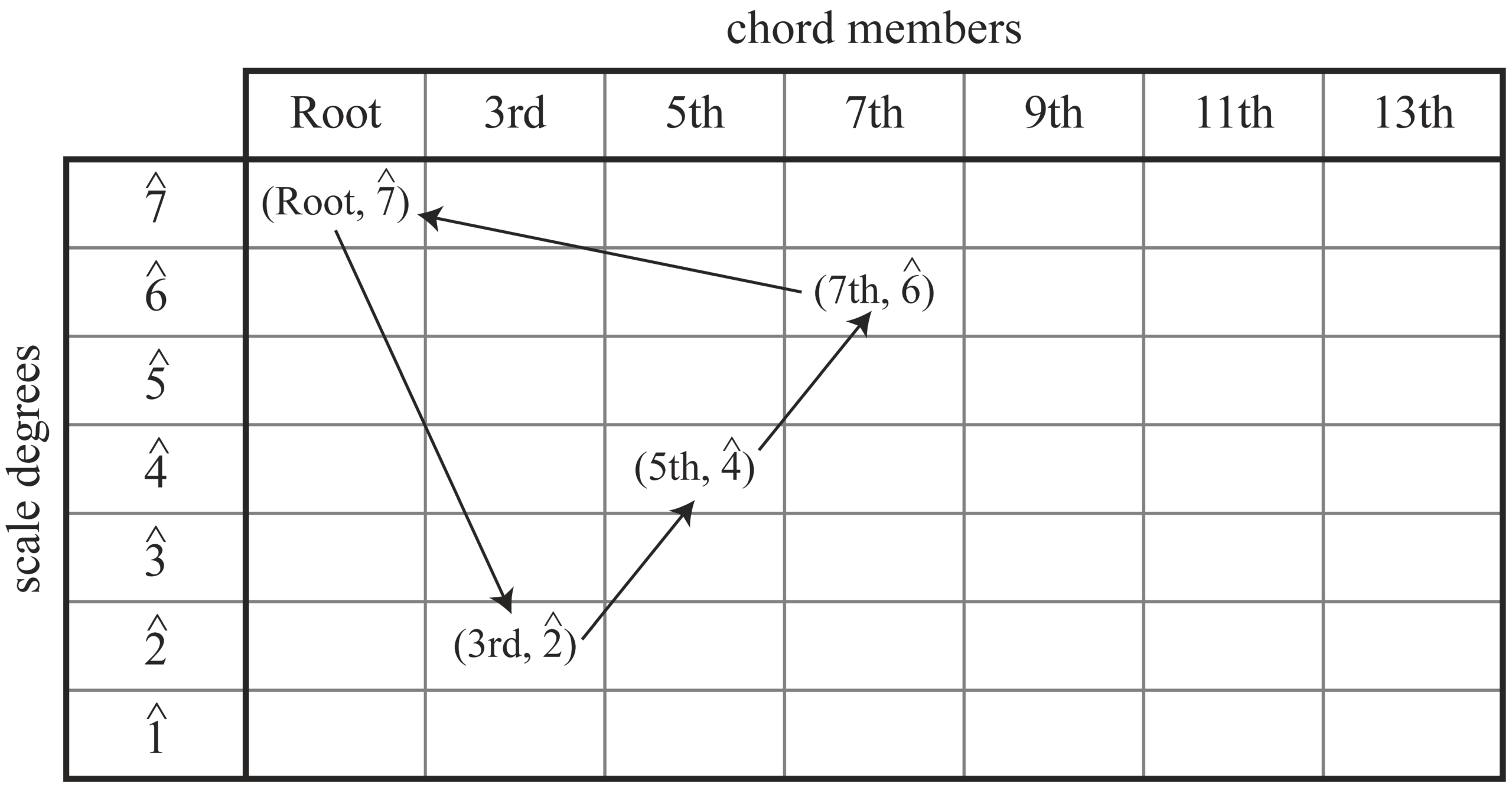
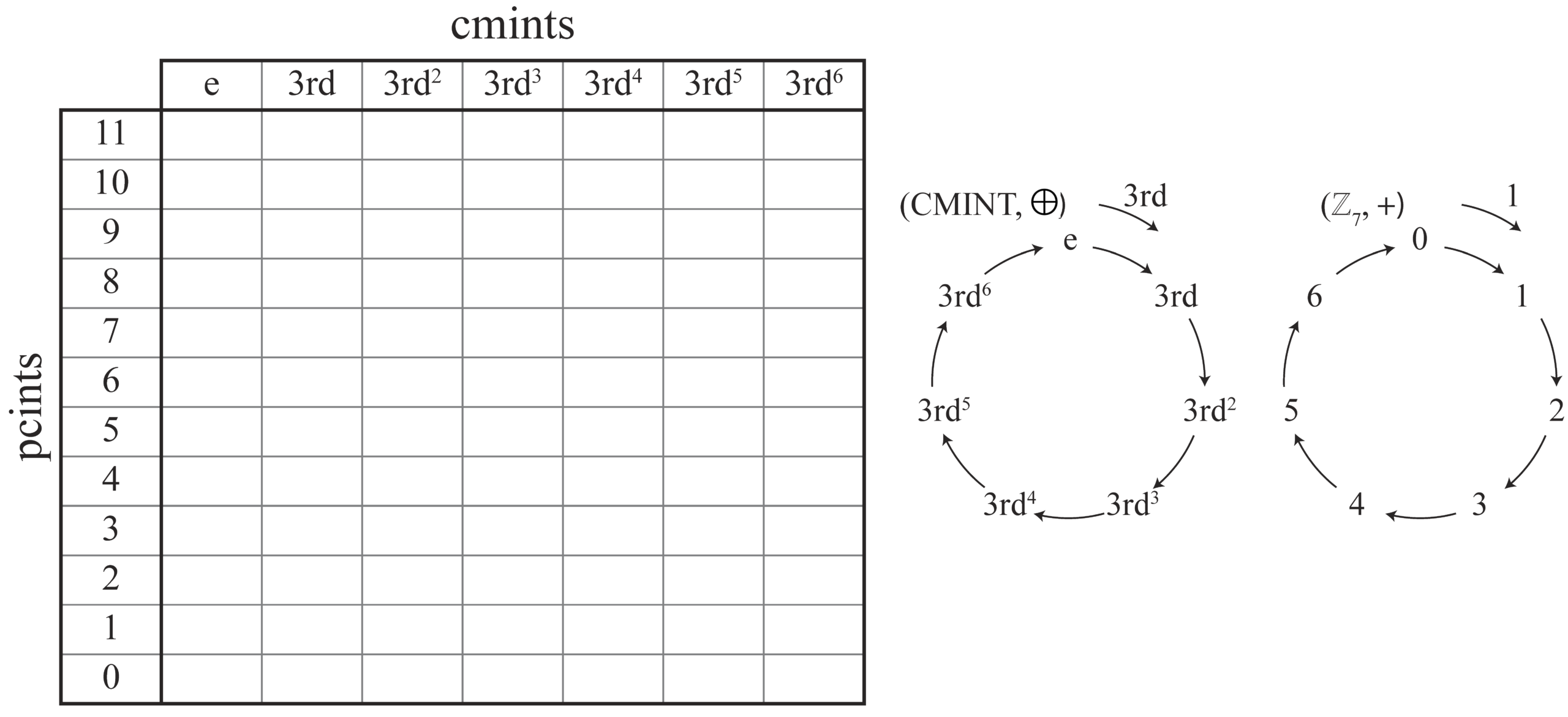
The group of intervals acting on cm is isomorphic to ℤ₇. We will refer to the group of intervals for cm as: cmint = {3rdⁿ | n ∈ ℤ₇} = {3rd⁰, 3rd¹, 3rd², …, 3rd⁶} = {e, 3rd, 3rd², …, 3rd⁶}. Additionally, we define the group operation ⊕ by 3rd^x ⊕ 3rd^y = 3rd^{x + y}. It is fairly straightforward to prove that cmint is a group under ⊕ (i.e., mod-7 addition) if we take a mapping f : ℤ₇ → cmint, where f (x) = 3rd^x for every x ∈ ℤ₇, and show that this mapping is an isomorphism between cmint and ℤ₇, a well-known group. We can come to this conclusion since the mapping is one-to-one and onto and the mapping preserves the respective group operations.

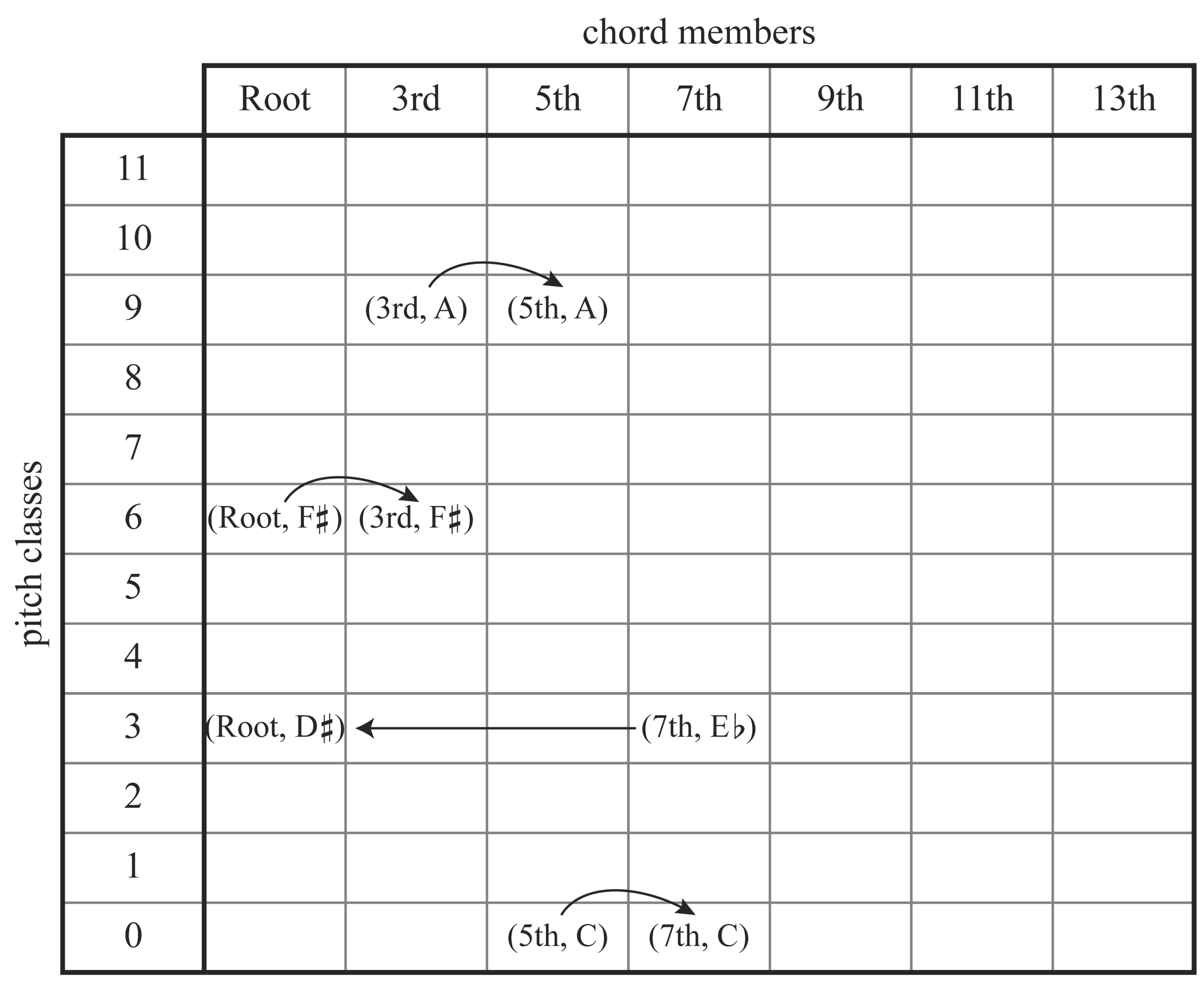
Example 4 demonstrates how the group of intervals acting on cm is not only isomorphic to ℤ₇ but is generated by the interval “3rd.” Since the group of intervals acting on pc is isomorphic to ℤ₁₂, the group of 84 intervals acting on cm × pc (defined as our interval group g) is isomorphic to ℤ₇ × ℤ₁₂, which itself is isomorphic to ℤ₈₄.

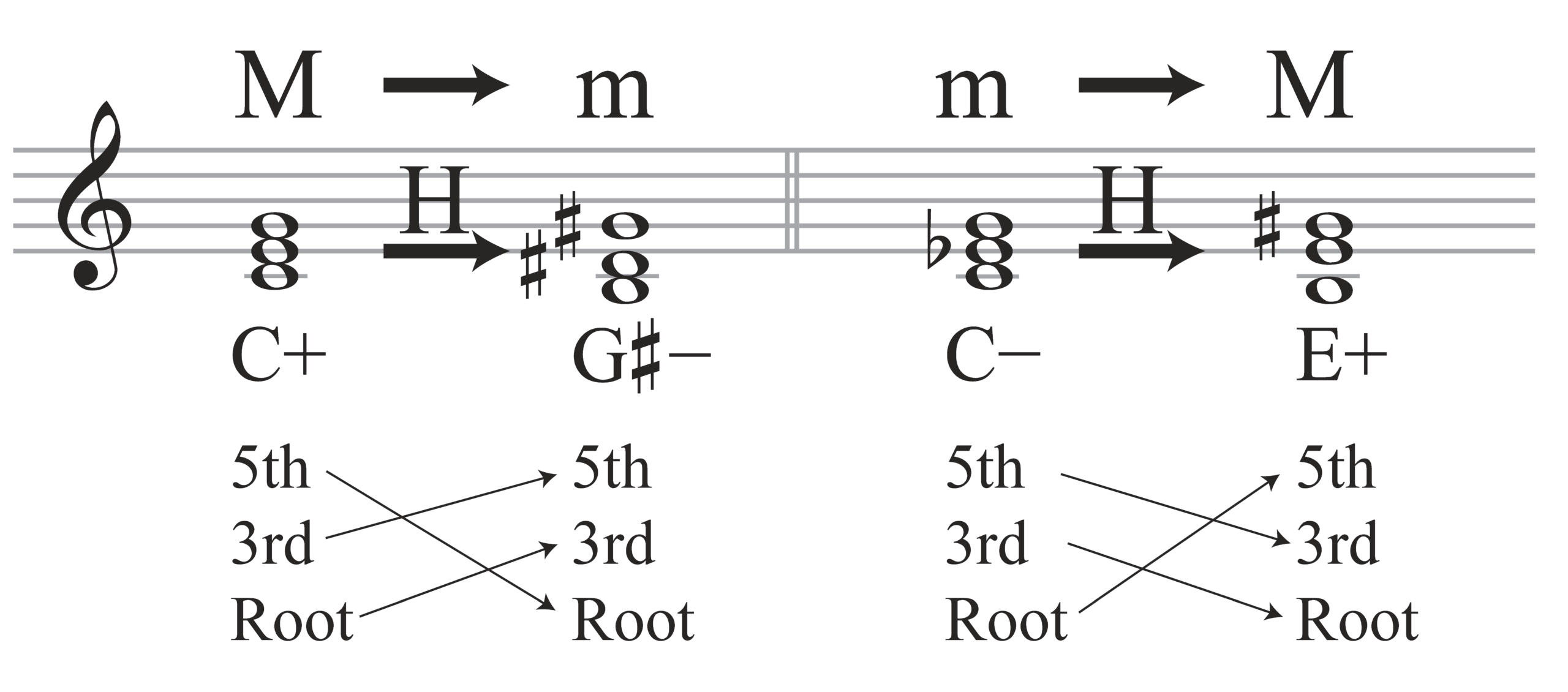
This system can describe motion between chords of different qualities, such as major and diminished triads. It can also describe motion between chords of different cardinalities, such as triads and seventh chords, more generally. These transformational relationships are different from a cross-type transformation between triads and seventh chords, which transforms objects from one set or space to another without disrupting the structural integrity of either space (Hook 2007, 3). Where my approach differs is through the basic assumption that the members of tertian chords of differing qualities and cardinalities exist in the same space, and that individual voices can and do move freely from one chord to another without respect to these discrepancies.

That being said, for simplicity, this system can be adapted to suit different tertian contexts. For example, we could adapt cm to a mod-3 space to analyze chords within a strictly triadic environment or to a mod-4 space if dealing with an environment that strictly uses seventh chords or some combination of triads and seventh chords. In such cases, we can refer to these respective spaces as cm₃ or cm₄. A similar proof as the one indicated earlier would show that for a generic (mod-n) reduced chord-member space cm_n, where n is a positive integer less than or equal to 7, the group of intervals acting on cm_n, cmint_n, is isomorphic to ℤ_n. However, some details would need to be tweaked so as not to imply that the root of a triad is found a “3rd” above the fifth or that the root of a seventh chord is found a “3rd” above the seventh. We could still recognize these intervals as triadic and seventh-chord intervals, respectively, but perhaps an interval label other than “3rd” would better serve these purposes. In situations like this, I would suggest substituting the label “3rd” with “x.” In any case, this methodology engages with voice leading in ways that other established transformational approaches do not.

Finally, we have an interval function, which David Lewin ([1987] 2007, 16) pioneers: int(s, t) = i. Examples 5a and 5b feature the beginning of J. S. Bach’s Prelude No. 1 in C major, BWV 846 (1722), and visually integrate Lewin’s concept of the interval function with this space.⁵ Example 5a shows how intervals can be conceived within the same arpeggiated chord, and Example 5b demonstrates how intervals emerge among different chords and multiple independent voices.

3. A Chord Member’s “Heard” Function

When presented with a musical passage containing tricky chromatic modulations, music theorists often explain these modulations via enharmonic reinterpretations. It is important to understand that these respellings are not just for convenience; they also reflect how each voice is truly perceived. The melodic gesture is usually but not always represented by spelling. This tendency has implications for how musicians think about the scale-degree function of certain voices. Similarly, these voices can have spellings in terms of chordal placement that run contrary to their proper chord-member function. In general, the composer’s or editor’s choice to spell notes in a certain way affects my chord-member reading, but in some cases, the spellings may not be compatible with the actual chord-member qualia.

The fully diminished seventh chord is a typical sonority that undergoes enharmonic chordal repositioning which may or may not be reflected by spelling. It has a characteristic tritone located between the chordal third and chordal seventh, and it also has one located between the root and fifth. Additionally, the chord has the characteristic interval of the diminished seventh; as musical objects, these two intervals are commonly manipulated to achieve different outcomes. The following excerpt from the first movement of L. v. Beethoven’s Sonata Pathétique, Op. 13 (1798) (Example 6) finds two different instances of the same enharmonic chord resolving in different ways. The first instance (m. 134) finds an F$$\sharp$$$$^{\circ}$$$$4\atop3$$ (vii$$^{\circ}$$$$4\atop3$$ in G minor) resolving to a Gm⁶ (i⁶) (a completely typical resolution of a leading-tone diminished-seventh chord), and the second instance (m. 135) contains a reinterpreted D$$\sharp$$$$^{\circ}$$$$4\atop2$$ (vii$$^{\circ}$$$$4\atop2$$ in E minor) resolving to a cadential six-four chord in E minor. Because the chord is clearly established as F$$\sharp$$$$^{\circ}$$$$4\atop3$$ in m. 134, we initially hear it as such in m. 135. The E$$\flat$$ is the crucial note whose respelling as D$$\sharp$$ informs us of how we expect the chord to resolve. The transformations of the notes F$$\sharp$$, A, and C are all given by (3rd, 0), i.e., one ascending chordal step. Meanwhile, the reinterpretation of E$$\flat$$ into D$$\sharp$$ transforms its chordal placement down three positions, given by the interval (3rd⁻³, 0).⁶

As shown in Example 7, one can model the enharmonic repositioning as movement through cm × pc. To reiterate, the respelling is not just for convenience; a change in chord-member qualia would inform this reading, even if the respelling is not necessarily notated in the score. The shift in quale for E$$\flat$$ from 7th to Root tells us that it is more appropriate to spell it as D$$\sharp$$.

One could analyze a note’s heard chord-member function alongside its scale-degree function. The ordered pair (cm, sd) can be used for members of the space cm × sd, where sd denotes scale-degree space. The concept comes from Rings (2011, 44–45), and the label comes from Hook (2023, 16). Additionally, (cmint, sdint) can be used for members of the interval group governing the space. One could also expand these readings using ordered triples: (cm, sd, pc) for members of the space cm × sd × pc, and (cmint, sdint, pcint) for members of the interval group governing the space, cmint × sdint × pcint. Analysis through cm × sd × pc would be most straightforward in a diatonic context. Whenever I use ordered triples, I use x to designate the chordal-third movement to avoid confusion since scale-degree intervals take the form of ordinal numbers, such as 2nd, 3rd, etc.⁷ Again, incorporating scale degrees in a chord-member/pitch-class analysis may be feasible depending on the context. In Examples 6 and 7, the enharmonic reinterpretation of the diminished seventh chord can be explained by a complementary scale-degree reading in a situation where the diminished seventh chord acts as a pivot chord between the tonic triads of G minor and E minor. The E$$\flat$$, for example, would not only undergo a chord-member change from 7th to Root, but it would also undergo a scale-degree change from $$\hat{6}$$ in G minor to $$\sharp\hat{7}$$ in E minor. Example 8a shows the first resolution in G minor in m. 134 (again, a completely typical resolution of a leading-tone diminished-seventh chord), and Example 8b demonstrates the repositioning in m. 135 through cm × sd. As can be seen in Example 8b, when scale degrees are substituted for pitch classes, we simply see a rotation of ordered pairs in cm × sd that reflects the enharmonic reinterpretation.

The augmented-sixth chord is another typical sonority involved in enharmonic repositioning, since the German sixth is enharmonic to a complete dominant seventh chord (i.e., one with a Root, 3rd, 5th, and 7th) and the Italian sixth is enharmonic to an incomplete dominant seventh chord (i.e., one with a Root, 3rd, and 7th but no 5th). Like with the diminished-seventh chord, these enharmonic respellings usually change the spelling of a few notes, but they also change the chord-member positions of every note. It may seem tricky to identify the root of an augmented-sixth chord since they are so commonly found in the same position, where $$\flat\hat{6}$$ of the key or tonality is found in the bass. Daniel Harrison (1995, 172) writes that while many theorists avoid the issue of root identification regarding the augmented sixth, some theorists, such as Robert W. Ottman, have tackled the issue by analyzing the root of both the German and Italian sixths as $$\sharp\hat{4}$$. Harrison additionally notes that for his work, he “subscribe[s] provisionally to the notion that the most common bass positions of the three ethnic augmented-sixth chords function as their root positions” (172). I do not think that Harrison is implying here that the sixth found above the bass in an augmented-sixth chord is the thirteenth of the chord; it seems instead that he is using the term “root position” to mean more of a default position. So, can the different versions of the augmented sixth be in inversion if they almost exclusively occur in the default position?

Consider two sets of common labels for each augmented sixth. The first set, labeled “It⁺⁶,” “Fr⁺⁶,” and “Ger⁺⁶” (which are commonly found in tonal harmony textbooks like Burstein and Straus 2020, 274–276), is not concerned with the perceived inversions of each chord. However, the second set, labeled “It⁶,” “Fr$$4\atop3$$,” and “Ger$$6\atop5$$” (found in Laitz and Callahan 2023, 809–811), includes what we would traditionally use as figured bass symbols next to each abbreviated label. These conventions shed light on the ongoing conflict between Roman-numeral and figured-bass analyses that theorists compromise in practice and in pedagogy. Whereas Roman numerals are concerned with harmony and, therefore, harmonic roots, figured bass symbols are concerned with actual intervals found above the bass note.

But let us consider where the augmented-sixth chord comes from and how it typically functions. If we identify it as a chromatic expansion of the diatonic Phrygian half cadence, there becomes an easy argument to identify a logical root. Despite Harrison adopting the notion that the augmented-sixth chord’s most common position is its root position, his approach to considering chromatic harmonies as “assemblies of scale degrees” (1994, 58) points toward understanding an Italian sixth as an inflected iv⁶, a French sixth as an inflected ii$$4\atop3$$, and a German sixth as an inflected iv$$6\atop5$$. Because of the voice-leading projection of $$\flat\hat{6}$$ and $$\sharp\hat{4}$$, he considers all versions of the augmented-sixth chord as “essentially S-functioned” (115).

Take the end of Frédéric Chopin’s G-minor Prelude, op. 28, no. 22 (1839), shown in Example 9.⁸ Measure 39 finds a German augmented-sixth chord spelled as a diminished-third chord with the root of the inflected iv⁷ in the bass. The previous few measures find E-flat major tonicized through a repeated common-tone diminished-seventh chord resolving to VI⁶. Once we arrive at m. 39, E-flat major has been emphasized enough to where the sonority in m. 39 sounds like an applied dominant (V$$4\atop2$$/$$\flat$$II), so the C$$\sharp$$ found in the bass initially sounds more like a D$$\flat$$. So, its chord-member quale undergoes a repositioning; its initial appearance has the quale of a chordal seventh, but its resolution transforms how we hear it, making it now the root.

---

Exploring scale-degree space is also interesting in situations where chord-member qualia is understood to be unclear or mysterious. Lewin ([1987] 2007, 17–18) discusses perception and intuition as culturally defined phenomena that can be sharpened through analytical reflection. It may take time, practice, and increasing sensitivity to polish our perceptions. It may take even more time to refine our perceptions of chord-member qualia since chord members are highly contextual and not absolute, and they require an understanding of balance among multiple independent voices. As an example, let us examine the opening few measures to Hugo Wolf’s song “Das verlassene Mägdlein” (1888), shown in Example 10. The opening harmonic progression almost does not make the A-minor tonality clear. While the pitch-class collection used is largely diatonic to the A-natural-minor scale, our tonal perception of A minor is most clearly shaped by the presence of the G$$\sharp$$ as the leading tone in m. 4.

Meanwhile, the piano’s sparse texture causes some issues with chord-member perception. The four introductory measures each find a dyad. The {F, A} dyad in m. 1, the {D, F} dyad in m. 3, and the {E, G$$\sharp$$} dyad in m. 4 all seem to be tertian, but they are all missing a third note that would clarify their chordal status. For example, should we hear mm. 1 and 3 jointly as a D-minor triad? Or are we to assume in each case that what is missing is the chordal fifth rather than some subposed chordal root? If we take the former approach, whereby mm. 1 and 3 are a joint D-minor triad, then we should hear each of the two voices moving down by chordal third. If we take the latter approach, where m. 1 is interpreted as an incomplete F-major triad and m. 3 is interpreted as an incomplete D-minor triad, then we should hear each of the two voices maintaining their respective chordal positions. Example 11 shows the difference between the interpretations. Since an A-minor tonality is clarified by the G$$\sharp$$ in m. 4, we are able to consider these various functional interpretations.

Additionally, the {A, B} dyad in m. 2 could very well imply a seventh chord, if we assume we are dealing with tertian harmony. Alternatively, one could read the first three measures together as an implied ii^ø7 harmony that forms a descending-fifths relationship with the V in m. 4.⁹ Example 12 shows this interpretation.

Lastly, the dyad in m. 5, where the singer enters, could imply the tonic triad, especially since the previous phrase ends on the dominant; the perception of A as tonic and as root can exist just as strongly as an actual played or sung A. Example 11 above shows the implied A. So, the functionality of these dyads largely relies on our perceptions. Harping on Lewin’s point again, we can gradually refine our experience of these few measures. This is arguably more true with chord members because chord-member qualia can be subjective. Our refined experience through chord-member analysis challenges us to identify tricky phenomena, such as the passage’s harmonic rhythm or chordal salience. The tonal information we gather can be useful additional information to enhance our experience.

4. Melodic Implications: Franz Schubert, “Die junge Nonne,” D. 828 (1825)

This section of the paper illustrates the efficacy of chord-member transformations by considering larger musical sections; indeed, this methodology helps track the activity of a prominent melodic note throughout the entire context of a piece. Take Franz Schubert’s “Die junge Nonne,” for example (1825). David Kopp (2002, 254) notes that Schubert’s song is a prime example of mediant-based harmonic relationships that clarify the overall musical structure and enhance textual meaning. Since the note F is the tonic of the overall piece and the highest note the vocalist sings, it is advantageous to track the chord-member intervallic motion of the sung high F over some of these harmonic mediants. The F, in particular, is repeatedly found in the somewhat static vocal line, so Schubert strategically writes it in harmonically diverse contexts. Example 13 shows a recreation of Kopp’s analysis of the F’s chordal placement in every instance. This new table includes information about the combined chord-member, scale-degree, and pitch-class motion every time the singer approaches F.

            Several of these approaches to F occur in mm. 54–61, as notated in Examples 14 and 15. Example 14 gives the score, and Example 15 analytically isolates each approach to F. Since the passage exhibits a clear global tonic and clear local tonics, I include the scale degree for each note and the scale-degree intervals for the overall three-part interval between two notes. This section of the piece transitions out of the F-minor Tempesta-like style of the first half of the piece to a calmer F-major mood. The first instance of the high F occurs in mm. 54–55, where the text reads, “In my heart is peace, in my heart is calm.” This moment is where the F acts as the dissonant seventh to the V⁷ of C major, preceded twice by the melodically-held fifth of the chord. This interval is given by (x, 3rd, 3), a simultaneous chord-member step and melodic skip within the same harmony.

The next set of instances of the F occurs in mm. 57–58 and then again in 58–59. In these measures, the text reads, “purified in the testing flames.” In the first instance, the voice moves up a semitone from E, the leading tone of the key, to F. The E is supported as the fifth of the A-major harmony, and the F is the root of the V⁷ of B$$\flat$$ major. Then, the voice maintains a perfect unison between mm. 58 and 59. The two measures have a common melodic tone, but the F’s placement changes from the root of the V⁷ of B$$\flat$$ to the fifth of B$$\flat$$ major. Here, there is a simultaneous chord-member skip with a perfect unison. This reading encourages us to hear this seemingly stagnant interval as only partially so.

Finally, the approach to F from m. 60 to m. 61 is a solid cadential moment where the voice moves from the third of V⁷ to the root of I on the words “betrothed to eternal love.” This semitone motion is distinct from the earlier one (mm. 57–58) since the voice moves via a chord-member step rather than a skip. In the first example, the E is supported by an A-major harmony; in the second, the E is supported by the dominant C⁷ harmony. The added chord-member interval highlights the harmonic difference between the two Fs, contrasting with the similar melodic motion. The chord-member transformations implicitly illustrate contrapuntal motion among the voices in question. The counterpoint in question is between that particular voice (in this case, the melody) and whatever the perceived root of the chord is (which one might describe as the fundamental bass). Furthermore, the contrast between the two transformations illustrates the strength of the E as the leading tone; its resolution is more substantial when supported by the descending-fifth motion in the bass rather than by descending third.

My added chord-member analytical layer shows the individual gestures performed at every approach to F, enhancing Kopp’s (2002, 261) argument that the note is experienced differently in each moment and expressing each instance’s unique character. This section’s proliferation of F solidifies the resolve of the persona singing the text; the young nun has made it through the mighty storm and prepares for a life of serving God.

5. Contrapuntal Implications: Frédéric Chopin, Etude in A$$\flat$$ major, Op. 25, No. 1

Shifting focus from melodic implications to contrapuntal analysis highlights the versatility of chord-member transformations in elucidating contrapuntal relationships amidst tonal ambiguity. Here, I analyze the chord-member transformations of mm. 22–25 of Frédéric Chopin’s Etude in A$$\flat$$ major, op. 25, no. 1 (1836–1837), which is reduced to block-chord form in Example 16. The difficulty in determining the tonality of the passage affects any attempted scale-degree reading. The overall piece is in A$$\flat$$ major, but these measures suggest something very different locally. The score clarifies the organization of each chord: some are in root position, some in inversion. Of particular interest is the G$$\sharp$$ on the fourth beat of m. 22. In some editions, this note is printed as A$$\flat$$ (perhaps to anticipate the resolution to G in m. 23), but I denote it in Examples 16 and 17 as G$$\sharp$$ to reflect its chordal-third quale in the E⁷ chord.¹¹

The top half of my chord-member transformational analysis in Example 17 reveals that three of the four progressions utilize double voice exchanges through this interpretation. The other uses a simple translation of the voices, meaning that the voices shuffle chord-member positions as though they were moving in a straight line, with the seventh circling back to the root. This system shows that these three chord successions use the same chord-member mappings even though other perspectives would maintain that they do not all share the exact mapping. The G$$\sharp$$$$^{\circ}$$⁷ in m. 23 that substitutes for the previous B$$^{\circ}$$⁷ in m. 22 utilizes the same voicing as its enharmonic equivalent. However, Chopin’s decision to spell the chord this way affects the overall chord-member repositioning. Regardless of how one hears this diminished seventh chord, this analysis provides two scenarios: one in which B is the chord’s root and the other in which G$$\sharp$$ is the root. One could even hear both measures with a root of B or both measures with a root of G$$\sharp$$. This analysis shows us enough contrast in the transformational voice-leading implications, even in the context of what would seem like two measures identically realized on an equal-tempered piano. My analysis of these measures highlights continuity in the passage, even within a landscape of tonal ambiguity.

Scholars note that as a perfectly even sonority, the diminished seventh chord is sometimes better suited as a gateway between octatonic sets of seventh chords rather than as a musical object with its own clear identity (Douthett and Steinbach 1998, 255; Cohn 2012, 155–158). It is thus unclear what the root of a diminished seventh chord might be. So, let’s suppose that the diminished seventh chords in this passage are rootless or part of a larger hidden sonority, namely, a dominant $$\flat$$9 chord. Let’s also assume that the chords’ current spellings reflect the true hidden roots (that is, the missing note that would complete a dominant $$\flat$$9 chord): for example, in m. 22, the chord spelled {B, D, F, A$$\flat$$} would have a root of G, but in m. 23, the chord spelled {G$$\sharp$$, B, D, F} would have a root of E. In the last measure, the note in the top voice, which I labeled a dissonant passing tone, can now be considered the root of such a sonority. In each case, the overall contrapuntal implications slightly change: where there originally were double voice exchanges are now exchanges of pairs of notes, and where there originally was a translation of voices is now a partial translation. This leads us to perceive the second interpretation as contrapuntally looser than the first. This contrapuntal looseness is attributed to the fact that the first interpretation deals strictly with the chord-member designations “Root,” “3rd,” “5th,” and “7th,” and each position is assigned to a single voice in every chord (meaning that there is a one-to-one correspondence between the chord members and the pitch classes of each chord). However, the second interpretation creates ambiguity due to the inclusion of the “9th” designation coupled with the fact that not every chord-member position is assigned a voice (indicating that there is not a one-to-one correspondence). The second interpretation, therefore, creates more complex chord-member counterpoint.

Some of these interpretations, of course, are subject to personal experience and perception. If I wanted to hear the diminished seventh in mm. 22–23 as part of a ninth sonority, I would be more inclined to hear them both as notated in m. 23 so that the top voice distinctly has the ninth of the chord. Notions of superposition and subposition, not unlike what Jean-Philippe Rameau proposes as a part of his fundamental bass theory (Lester 1992, 108–114), can be justified through experience. In this case, one can hear the diminished-seventh chord in mm. 22–23 with a subposed root of G or E via expectation and refined listening.

The extended analyses presented in this article emphasize the transformative potential of chord-member analysis in enriching our understanding of chord progressions and voice leading, paving the way for further exploration across diverse musical repertoires.

6. Applications to Neo-Riemannian Theory

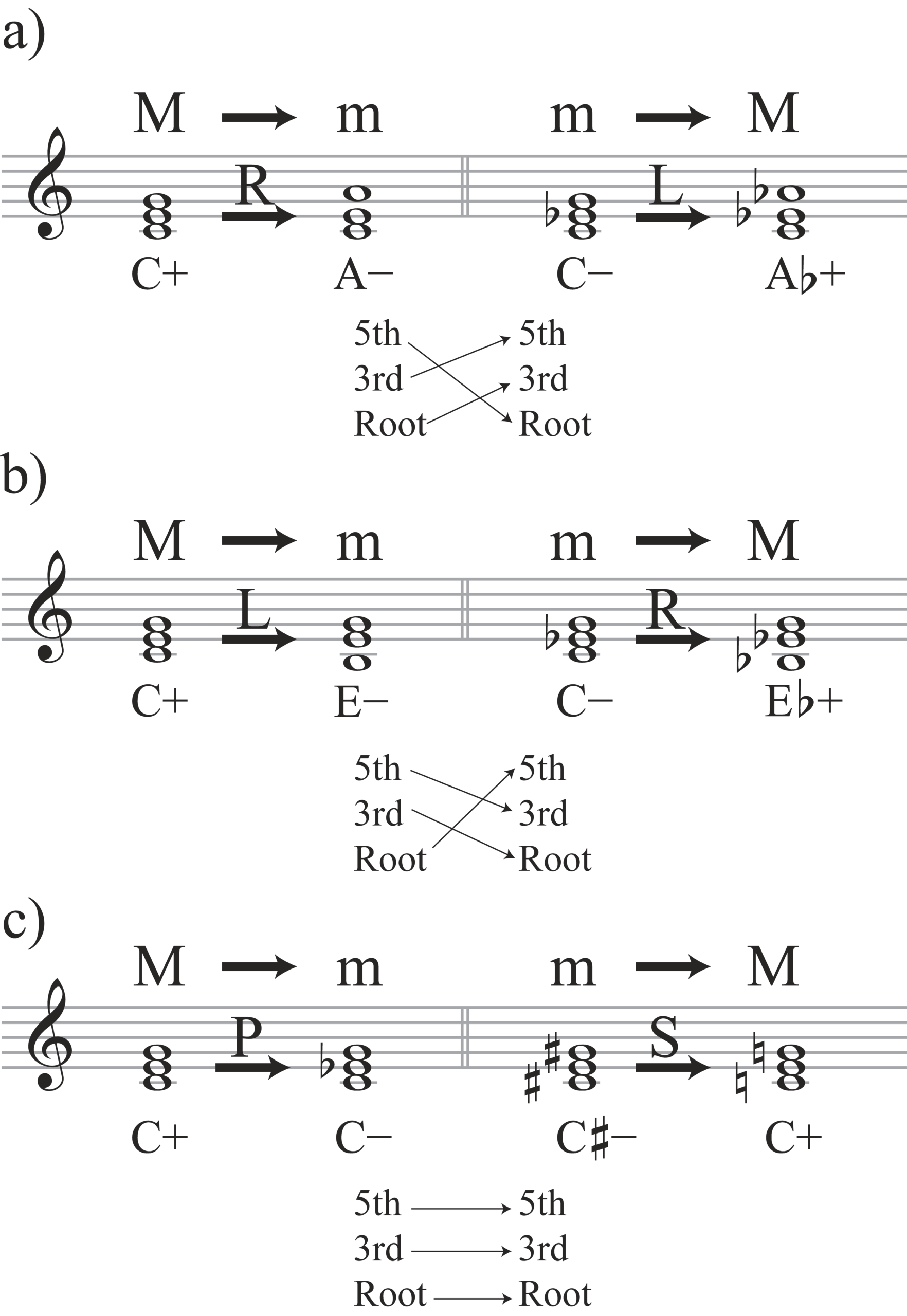
Chord-member transformations can also reveal similarities among voice leadings that might seem different on a surface level. For instance, this transformation system can highlight intriguing features that are shared by various neo-Riemannian operations, which invert triads from major to minor and vice versa (Cohn 1997). Like neo-Riemannian analysis, chord-member transformational analysis does not require knowing the tonality of a musical setting. Despite neo-Riemannian operations being considered “contextual” inversions, these operations are not deferent to any tonal center.¹² Example 18a shows parsimonious voice leading between C-major and A-minor triads, a typical example used to introduce neo-Riemannian theory, specifically, the operation “R” for “relative.” Here, the C-major triad maintains two common tones; the C and E stay stationary while the G moves up by a whole step to A. However, this causes each voice to reposition itself within the triad, signaling individual movements within cm. The C moves from its position as the root of the first triad to the third of the next, and the E moves from the third of the first triad to the fifth of the next. As a result, the (cmint, pcint) intervals for the C and E are both given by (3rd, 0). This interval indicates a simultaneous ascent in cm and stagnation in pc.

Meanwhile, the G moves up a whole step to A while also moving from the fifth of the C-major triad to the root of the A-minor triad. Therefore, the interval describing this motion is (3rd⁻², 2), an indication of a simultaneous descent in cm and ascent in pc.¹³ This interval has implications for the dynamic ways that voices move linearly against a backdrop of vertical locations.¹⁴

This system reveals a similarity between the R operation acting on a major triad and the L operation acting on a minor triad, as shown in Example 18a. Moreover, these two operations have similar chord-member motions as their respective R and L counterparts in Example 18b: two voices shift by one chordal third, and the third voice shifts in the opposite direction by two chordal thirds. The system sees no effect, however, on the Parallel (“P”) or SLIDE (“S”) operations in Example 18c. One reason is that the P and S operations shift one or two voices by a chromatic semitone, leaving the chord members unchanged. In contrast, the R and L operations shift one voice by a diatonic semitone or whole tone, affecting each voice’s chordal position. In other words, the P and S operations preserve the overall tertian structure, whereas the R and L operations do not. As stated earlier, this distinction in spelling between diatonic and chromatic semitones reflects the perceptions of each changing chord member. The chord-member qualia do not reflect the spellings, but the spellings usually reflect the qualia.

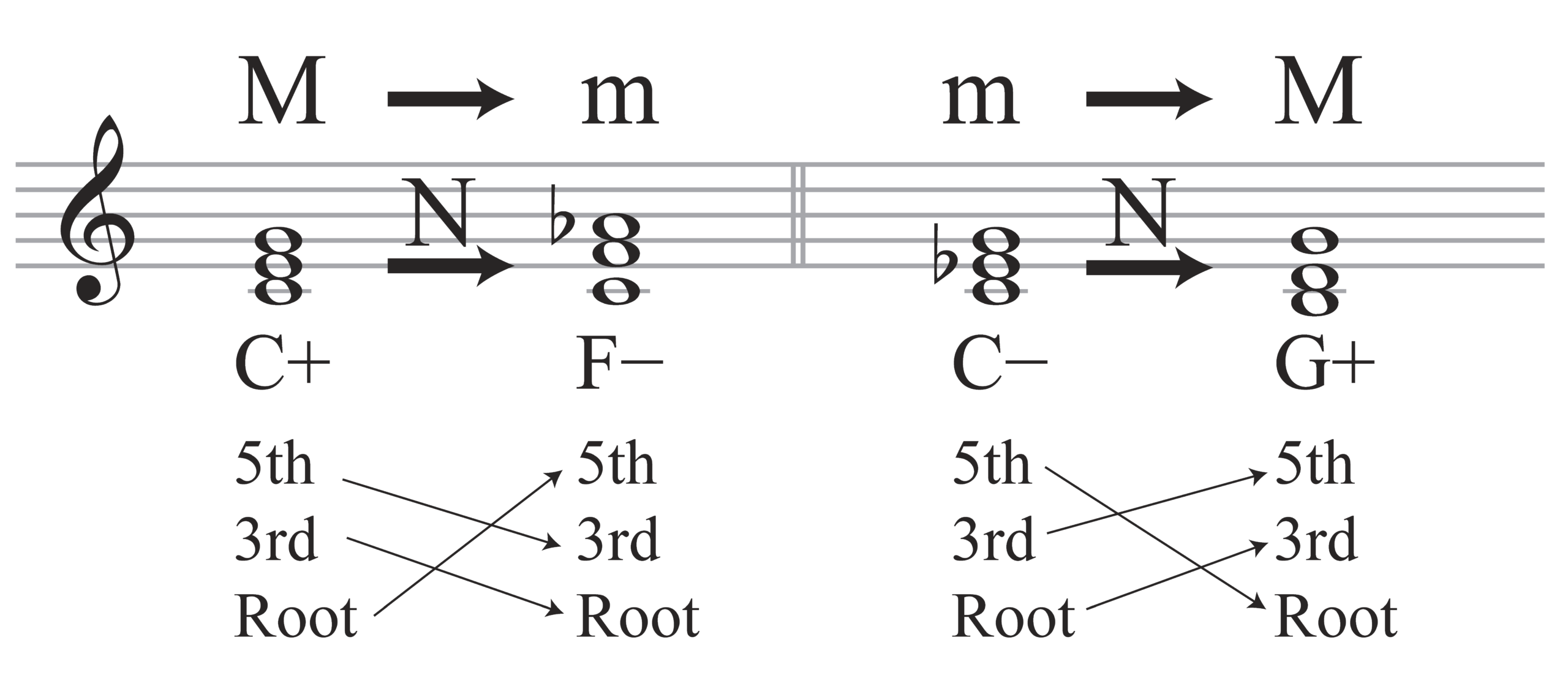
Two other common neo-Riemannian operations can be generalized in this way. First, the Nebenverwandt (“N”) operation, shown in Example 19, maps a major triad (C major) onto what we think of as its minor subdominant (F minor) and maps a minor triad (C minor) onto what we think of as its major dominant (G major). The former (C major to F minor) joins the group of transformations in Example 18b, and the latter (C minor to G major) joins that of Example 18a.

Second, we have the hexatonic pole (“H”) operation, which is a special case. Example 20 shows the operation below. On one hand, it can be analyzed similarly as above: it joins the group of transformations in Example 18a when a major triad transforms parsimoniously into a minor triad, and it joins that of Example 18b when a minor triad transforms parsimoniously into a major triad.

Example 21, displaying a well-known progression in Act III of Richard Wagner’s Parsifal (1882), shows how the H operation can be analyzed through a chord-member perspective in a similar fashion as another operation (in this case, L). The progression is a descending major-third cycle of triads, but each successive triad changes quality. Since both of the H operations transform a major triad into a minor triad and the one L operation transforms a minor triad into a major triad, all three neo-Riemannian operations undergo the same chord-member transformations. My transformational reading observes four distinct voices in the texture, including the bass voice that serves as the root to each sonority. Each of the upper voices, on the other hand, travels through one of the following loops: “Root → 3rd → 5th → Root,” “3rd → 5th → Root→ 3rd,” or “5th → Root→ 3rd → 5th.”¹⁵

On the other hand, the operation may present some ambiguous heard chord members because it is highly chromatic; that is, since every voice is displaced by semitone, it is as maximally smooth as it can be without maintaining any common tones.¹⁶ Take the following excerpt (Example 22a) from Franz Liszt’s Polonaise I (1875; from S. 519/1, transcribed for piano from Die Legende der heiligen Stanislaus, S. 688), which Richard Cohn (1996, 25–30) uses as one example to introduce hexatonic cycles and polarity.

Cohn divides this section by hexatonic regions: mm. 98–101 contain triads in the HEX₃₄ group, mm. 102–105 contain triads in the HEX₁₂ group, and then each of the three following measures (106–108) alternates between HEX₃₄ and HEX₁₂ via transposition until mm. 109–110, where the key of E major is more firmly established with a cadence.

The first four measures demonstrate this H operation between the E-major and C-minor triads. Given the slow tempo of the excerpt (dotted quarter = 48) and that the harmonic rhythm is equal to a dotted whole note, each triad sounds for several seconds. It is possible to hear these four measures as an alternation between the two consonant triads, but this longer amount of time taken between measures allows our ears to adjust and hear the notes as tendency tones leading into the next measure. With a harmonic reduction shown in Example 22b, one may be inclined to hear each E-major triad leading to a C-minor triad (mm. 98 and 100) as a collection of tendency tones. The E becomes reinterpreted as F$$\flat$$ and the G$$\sharp$$ becomes reinterpreted as A$$\flat$$. Similarly, in m. 99, where C minor leads back to E major, the E$$\flat$$ gets reinterpreted as D$$\sharp$$ and the G as F_𝄪. In each case, the chords aurally change from consonant triads to more dissonant sonorities; the former may be described as a diminished-seventh chord with a diminished chordal fifth and a missing chordal third, and the latter may be referred to as a diminished-seventh chord with a major chordal third and a missing chordal fifth. Example 22c shows a similar situation as Example 22b, just transposed up a major second. As shown in both Examples 22b and 22c, one level of structure (the light gray dashed arrows) reflects more seamless chord-member reassignments between consonant triads, whereas the other level (the solid black arrows) reflects more activity in chord-member reassignments when we hear one of said triads as dissonant.

Finally, mm. 106–108 present a series of H operations at successive levels of whole-step transposition. Shown in Example 22d, one can make a similar case for each major triad moving to its hexatonic pole. The chord-member motions are only explicitly shown in the first measure, but they are exactly the same across all three.

It follows, then, that certain neo-Riemannian operations have similar chord-member voice-leading schemas, and we can use chord-member analysis to generalize about the uniqueness of voice leadings. Focusing on the schema of chord-member-to-chord-member motions reveals similarities among progressions that otherwise would be described as different. In mm. 98–99 in Liszt’s Polonaise, for instance, the overall chord-member schema from E major to C minor would be preserved if m. 99 had instead been written as C-sharp minor. Example 23 shows this difference. Despite E major and C-sharp minor having a diatonic-third relationship and E major and C minor having a chromatic-third relationship, and despite the fact that C minor and C-sharp minor are a semitone apart, the voices of the chords do not change their overall chord-member placements.¹⁸

7. Some Notes on the GIS and Broader Relevance to Transformational Theory

With the full introduction of the system now comes some notes of caution about this system. I do not mean to undermine the system; I am merely highlighting areas where the system can be misused and suggesting that there are opportunities for further research.

First, registral placement is sometimes a consideration in this space. A chordal third can appear as a simple or compound third above the root, and one can even find unique arrangements of chord members in the case of chordal inversions or special voicings. However, this same principle is not implicit with other chord members. One should not reduce chordal ninths to a second above the root, and one should not mistake a dissonant fourth above the root as an eleventh. For the extended tertian members (ninths, elevenths, and thirteenths), the harmonic syntax must support their status as members of a tertian harmony. Usually, three of the four lowest chord members (Root, 3rd, 5th, and 7th) must also be clearly articulated to support the extended chord members. This GIS is based on tertian relationships, with the harmonic third as the fundamental building block. Therefore, few gaps can be left between non-consecutive chord members. In late-nineteenth-century chromaticism, the extended tertian members are typically found in the top voice of a given texture, and they are usually extensions of the dominant harmony and thus have standard resolutions. So, a chordal ninth can be realized in musical textures as a ninth, sixteenth, twenty-third, etc., above the root.

Second, in order for one to use this space in a meaningful capacity, the musical context must clarify the tertian chord structure. This means that note-spelling matters, for it usually informs us of a note’s chord-member quale. Since the musical context must make the tertian chord structure clear, it follows that not every generic pitch class found in some generic pitch-class set can be assigned a generic chord-member location, even though one could theoretically create a one-to-one correspondence between gpc and cm. Doing so would create an unnecessary conflation between abstraction and experience. Again, the context must make this explicit.

Thus, while there are similarities between gpc and cm, the ways one navigates these spaces have notable differences. As Frederick (2019, 168) highlights in her exploration of generic (mod-7) voice-leading spaces, geometric voice-leading spaces associated with chord members are fundamentally discrete. Unlike the generic pitch classes with which Frederick works, chord members are highly contextual, and the implications of such voice-leading spaces would not be exactly analogous to what she has developed. For one thing, chord members as abstractions in a GIS may function as independent elements, but they are not treated independently in actual musical practice. Take the following chord from Examples 16 and 17, for example: {E, G$$\sharp$$, B, D}. I discussed earlier that some editions of Chopin’s etude notate the G$$\sharp$$ in m. 22 as an A$$\flat$$, presumably to anticipate a resolution to G-natural in the following measure. However, I keep it notated as G$$\sharp$$ to reflect its quale as the chordal third. So, let us re-notate the chord as {E, A$$\flat$$, B, D}. Regardless of spelling, the elements become unequivocally reinterpreted as the generic chords {E, G, B, D} and {E, A, B, D}, respectively. When it comes to chord members, however, only one of these chords has a clear mapping: {E, G$$\sharp$$, B, D} is easily interpreted as {Root, 3rd, 5th, 7th}, but {E, A$$\flat$$, B, D} is not so clear. Perhaps it could be interpreted as {Root, ___, 5th, 7th}, where ___ is a dissonant, non-tertian chord member. Assigning A$$\flat$$ to the “3rd” designation would require a clear hearing of it as the chordal third. Because I hear it this way, I choose to notate it as G$$\sharp$$.

Because chord members are more contextual than generic note names, the “Root” identity will appear far more often in the applications of my methodology than any other chord-member identity, and few tertian sonorities will lack a root. It is possible, for instance, to create a theoretical chord-member dyad that strictly consists of a chordal third and a chordal eleventh, but one would be hard-pressed to find such a tertian structure in actual music. On the other hand, one could identify the notes of a diminished-seventh interval as the third and ninth of a V^$$\flat$$9, like in Example 17 shown earlier. Furthermore, depending on the musical context, some non-root chord members will appear less than others. In the analytical examples I provide in this article, drawn from eighteenth- and nineteenth-century Western art music, the extended tertian labels “9th,” “11th,” and “13th” hardly appear.

Lastly, it is worth reiterating that scale degrees are not a basic feature of cm, but as I show earlier, it can be useful to combine scale-degree analysis with chord-member analysis. The independence of chord members from scale degrees can be a virtue in musical situations where tertian chord structure is clear but tonal centers are not or where the tonal center is not an analytical concern (such as in neo-Riemannian analysis).

As stated at the beginning of the article, there are multiple musical parameters that one can explore through transformational analysis. These multiple perspectives arise because no transformational technique is wholistic or comprehensive. Every approach creates or utilizes different theoretical apparatuses, and each approach is based on different assumptions; these approaches, in turn, address gaps left by existing scholarship and create ways to solve the apparent issue. For example, Hook’s (2002) Uniform Triadic Transformations (UTTs) can help describe chord progressions that feature consonant (i.e., major and minor) triads or other progressions that feature the Tristan genus (Cohn 2012, 148–152). UTTs create a standard for describing Riemannian and non-Riemannian operations alike. However, additional methods (such as the cross-type transformation, mentioned earlier) might be needed to analyze progressions that feature a mixture of consonant and dissonant triads or a mixture of triads and seventh chords. Additionally, Richard Bass (2007) has theorized about irregular seventh-chord resolutions to triads in nineteenth-century chromatic music. Bass (2007, 83–88) devises a vocabulary in his article to describe the voice leading implied by these resolutions, manifested through enharmonic reinterpretations that reorganize the seventh chords. While I have tackled similar issues as Bass, such as enharmonic reinterpretation, my approach does not systematize the exact semitonal displacement between a dissonant seventh chord or augmented-sixth chord and its triad of resolution. My approach is based on experience and perception within a generalized tertian space, for I argue that our ears can perceive these tertian relationships and changes.

Tymoczko (2023, 132–137) also discusses experience when describing the phenomenon of “thinking within the chord,” where one conceptualizes the notes of a given chord as its own musical space. He describes it using the following analogy:

One can imagine a metaphorical harp (or autoharp) sounding a chord’s notes in every octave, providing a field of contrapuntal play. Those slots shift as the chord changes, typically by efficient voice leading; the surface voices’ motion-within-the-chord is unperturbed by the shifts, like a melodic sequence inside a modulating scale. This description resonates with the Schenkerian insight that voice leading often takes place in a musical “background” simultaneously real and yet not always obvious in the score. More specifically, it allows us to implement the Schenkerian strategy of relegating doublings and voice exchanges to the surface, as artifacts of voices moving within a simpler background. (Tymoczko 2023, 134–135)

While there is some overlap between our approaches, there are two main ways that they differ. First, my approach arranges chord-member labels in a generic (mod-7) structure, whereas Tymoczko is still primarily concerned with a chord’s pitch classes. Second, unlike my approach, Tymoczko’s is not limited to tertian chords, though he spends a great deal of time applying his idea to such structures and drawing attention to significant changes in chord-member positions. By focusing on transformational relationships between tertian chord positions, my approach allows the analyst to individualize these musical gestures and contextualize them in a delicate yet immaculate contrapuntal environment. One can think “within” a single tertian chord and among multiple chords; my approach encourages us to think within a generalized chord.

Conclusion

In this article, I have presented a new approach to examining changes in chordal placement as individualized musical gestures. Doing so requires devising a generic (mod-7) space in which an individual voice may be located and giving said voice the agency to move around in that space. One can use this approach to track the motion of a single melodic voice or a group of voices acting together contrapuntally.

Lewin ([1987] 2007, 159) writes that the transformational attitude embodies a persona inside the music in the absence of an external observer, noting the following about conceptions of space in which intervals and transformations lie:

In conceptualizing a particular musical space, it often happens that we conceptualize along with it, as one of its characteristic textural features, a family of directed measurements, distances, or motions of some sort. Contemplating elements s and t of such a musical space, we are characteristically aware of the particular directed measurement, distance, or motion that proceeds “from s to t.” (Lewin [1987] 2007, 16)

Rings (2011, 37) further adds that Lewin does not describe intervals and transformations as “things in the world, but as relationships actively construed and apperceived by an individual in contact with some musical phenomenon.” The transformational system I have introduced allows one to navigate vertical, chordal position in a linearized fashion. As we consider interdependence and independence of lines in harmony and counterpoint, this system challenges us to consider how voices change their vertical location in moving from note to note and chord to chord.

The previous analytical examples show the voice-leading implications of this heard chord-member transformation system. This system offers a newly instructive way of thinking about chord progressions and provides an illustrative reading of voice leading that occurs when chordal voices reposition themselves. In so doing, this approach closely reflects the transformational attitude.

---

References

Bass, Richard. 2007. “Enharmonic Position Finding and the Resolution of Seventh Chords in Chromatic Music.” Music Theory Spectrum 29, no. 1: 73–100.

Burstein, L. Poundie, and Joseph N. Straus. 2020. Concise Introduction to Tonal Harmony. 2nd ed. New York: W. W. Norton & Company.

Callender, Clifton, Ian Quinn, and Dmitri Tymoczko. 2008. “Generalized Voice-Leading Spaces.” Science 320, no. 5874: 346–348.

Clough, John. 1979. “Aspects of Diatonic Sets.” Journal of Music Theory 23, no. 1: 45–61.

———. 1979–1980. “Diatonic Interval Sets and Transformational Structures.” Perspectives of New Music 18, nos. 1–2: 461–482.

Cohn, Richard. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions.” Music Analysis 15, no. 1: 9–40.

———. 1997. “Neo-Riemannian Operations, Parsimonious Trichords, and Their ‘Tonnetz’ Representations.” Journal of Music Theory 41, no. 1: 1–66.

———. 2012. Audacious Euphony: Chromaticism and the Triad’s Second Nature. Oxford: Oxford University Press.

Douthett, Jack, and Peter Steinbach. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition.” Journal of Music Theory 42, no. 2: 241–263.

Frederick, Leah. 2019. “Generic (Mod-7) Voice-Leading Spaces.” Journal of Music Theory 63, no. 2: 167–207.

Harrison, Daniel. 1994. Harmonic Function in Chromatic Music: A Renewed Dualist Theory and an Account of Its Precedents. Chicago: University of Chicago Press.

———. 1995. “Supplement to the Theory of Augmented-Sixth Chords.” Music Theory Spectrum 17, no. 2: 170–195.

Hook, Julian. 2002. “Uniform Triadic Transformations.” Journal of Music Theory 46, no. 1/2: 57–126.

———. 2007. “Cross-Type Transformations and the Path Consistency Condition.” Music Theory Spectrum 29, no. 1: 1–40.

———. 2023. Exploring Musical Spaces: A Synthesis of Mathematical Approaches. New York: Oxford University Press.

Kopp, David. 2002. Chromatic Transformations in Nineteenth-Century Music. Cambridge: Cambridge University Press.

Laitz, Steven G., and Michael R. Callahan. 2023. The Complete Musician. 5th ed. New York: Oxford University Press.

Lerdahl, Fred. 2001. Tonal Pitch Space. New York: Oxford University Press.

Lester, Joel. 1992. “Rameau’s Early Works.” In Compositional Theory in the Eighteenth Century, 90–126. Cambridge, MA: Harvard University Press.

Lewin, David. [1987] 2007. Generalized Musical Intervals and Transformations. New York: Oxford University Press. Original publication, New Haven, CT: Yale University Press.

Rings, Steven. 2011. Tonality and Transformation. New York: Oxford University Press.

Straus, Joseph N. 2016. Introduction to Post-Tonal Theory. 4th ed. New York: W. W. Norton & Company.

Tymoczko, Dmitri. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. New York: Oxford University Press.

———. 2023. Tonality: An Owner’s Manual. New York: Oxford University Press.

1. Steven Rings (2011, 37) mentions the potential conceptualization of an ideal chord-member space in discussing the impact of Lewin’s Generalized Musical Intervals and Transformations ([1987] 2007). However, he does not develop it beyond this brief mention.
2. Unless otherwise noted, I use the term “generic” in the mod-7 sense, similar to how Hook (2023, 15–16) uses the term to define generic pitch-class space (gpc) as “an abstract seven-note space that may alternatively be called letter space, as its elements are simply the unsigned letter names C, D, …, B.” Ultimately, this idea is rooted in John Clough’s (1979 and 1979–1980) diatonic theory.
3. One could argue that it is difficult to conceive a space of tertian chord positions without specific pitches or note names, and to some extent, I agree. That is why I later explain the advantage of examining both parameters simultaneously.
4. Rings (2011, 44–49) devises a GIS that describes “heard” scale degrees in tonal contexts. He also discusses the idea of tonal quale, a perception of a tone influenced by experience and requiring present reflection, particularly in the context of Western common-practice tonal music (41–43). This idea is critical to the applications of my work, though my approach does not require recognition of a tonal center.

   Rings’s GIS takes inspiration from David Lewin’s ([1987] 2007) definition of a GIS, which is an ordered triple of the from (s, ivls, int), where s is a space or family of elements, ivls (or alternatively, “g”) represents the group of intervals for the system, and int is a function that relates two elements from s to an interval from g.

5. Additionally, in Lewin’s ([1987] 2007, 26) work, for all r, s, and t in s: int(r, s)int(s, t) = int(r, t); and for every s in s and every i in g, there exists a unique t in s that satisfies int(s, t) = i.
6. Alternatively, we could describe this interval as (3rd⁴, 0) if we wanted to keep the chord-member interval numbers between 0 and 6 (i.e., mod-7). Here, I find the negative superscript to be more convenient for showing the chord-member exchanges among the four voices of a diminished-seventh chord.
7. In general, “x” will become a common substitute for the label “3rd” whenever clarity is needed.
8. Thank you to one of my reviewers for suggesting this piece.
9. To be frank, this seems to be the most likely explanation. If m. 3 is heard as a D-minor triad, the implied ascending-third motion from B (m. 2) to D (m. 3) would be unusual.
10. For reference, the intervals x and x⁶ (i.e., x⁻¹) are each considered “Chord-Member Steps,” x² and x⁵ (x⁻²) are “Chord-Member Skips,” and x³ and x⁴ (x⁻³) are “Chord-Member Leaps.”
11. Note that the two chords shown in m. 22 are played over a pedal tone C in the bass, which walks down independently to B in m. 23 and A in m. 24. This independent bass line is not accounted for in my upper-voice chord-member analysis until m. 25 when its semitonal shift down to A$$\flat$$ occurs, which mirrors the same upper-voice semitonal shift.

    Alternatively, the final E of each of mm. 22–24 (e.g., in the soprano voice in m. 22) could be considered an anticipation of the first E of the following measure, suggesting that not every verticality is a tertian chord. However, I tend to hear the soprano line in 4-note groups, where the fourth beat of each of these measures is the point of rest before beginning the 4-note pattern again. Thus, I find it appropriate to treat each simultaneity as a tertian chord.

12. For the reader’s reference, neo-Riemannian operations are often considered contextual inversions, whereby the “axis of inversion is determined by the context—by the position of the triad within pitch-class space” (Hook 2023, 120). These inversions are usually centered around a common note or interval between the two consonant triads (or major-minor and half-diminished seventh chords, i.e., what Richard Cohn refers to as the “Tristan genus”; 2012, 148–152).
13. Again, we could alternatively describe this interval as (3rd⁵, 2) if we wanted to keep the chord-member interval numbers between 0 and 6. Here, I find the negative superscript to be more convenient for showing the chord-member exchanges among the three voices of a generalized triad.
14. In cm₃, we would see the exact chord-member mappings but with slightly different interval labels. For voices that move from 5th to Root, for example, we can simply label that chord-member interval as x. So, the interval describing the motion in the top voice would be (x, 2).
15. Note that I consider the D₄ in the B-minor triad and the D₅ in the G-major triad to be from the same voice via octave displacement, and I indicate this in the diagram.
16. The H operation is particularly special because it yields every consonant triad’s hexatonic complement (i.e., the other three pitch classes included in a given hexatonic region).
17. I have changed the hexatonic collection labels “H₀” and “H₂” that Cohn uses in the original 1996 article to “HEX₃₄” and “HEX₁₂,” which are more standardized (Straus 2016, 257).
18. These chord-member schemas resemble what Tymoczko (2011, 45–49) argues about transpositional and inversional chordal relationships that highlight the uniqueness of voice leadings. He comments on the uniformity and individuality of voice-leading transpositions and inversions, but rather than exploring them through a GIS, he only implicitly explores them from the perspective of chord members.

    This reading also enables us to see this progression as an altered version of the familiar diatonic “ascending 5–6” sequence pattern.